Torus wars

L’algorithme d’Euclide

Calcul de PGCD

L’algorithme d’Euclide permet de calculer le pgcd de deux entiers de façon efficace. Étant donnés deux entiers $a > b$ , il procède comme suit:

Prendre $r_0 = a$ et $r_1 = b$ ;
Tant que $r_i$ n’est pas un multiple de $r_{i+1}$
- Calculer $r_i = k_i r_{i+1} + r_{i+2}$ par division Euclidéenne;
Le pgcd est le dernier reste non nul.

Exemple: Calculons le pgcd de 15 et 55

$r_0 = 55, r_1 = 15$ ,
$55 = 3\cdot 15 + 10$ , donc $r_2 = 10$ ,
$15 = 10 + 5$ , donc $r_3 = 5$ ,
$10 = 2*5$ , donc le pgcd de 15 et 55 est 5.

Exercices

Calculer le pgcd de 25 et 72;
Calculer le pgcd de 2244 et 1955;

Relations de Bezout

Le théorème de Bezout affirme que pour tous entiers $a, b$ , il existe des entiers $u,v$ tels que

$ua + bv = \gcd(a,b).$

L’algorithme d’Euclide étendu permet de calculer ensemble le pgcd de $a$ et $b$ et la relation de Bezout. Il procède de façon similaire à l’algorithme d’Euclide.

Prendre $r_0 = a$ et $r_1 = b$ ;
Prendre $u_0 = 1$ , $u_1 = 0$ , $v_0 = 0$ et $v_1 = 1$ ;
Tant que $r_i$ n’est pas un multiple de $r_{i+1}$
- Calculer $r_i = k_i r_{i+1} + r_{i+2}$ par division Euclidéenne;
- Calculer $u_{i+2} = u_i - k_i u_{i+1}$ ;
- Calculer $v_{i+2} = v_i - k_i v_{i+1}$ ;
Le pgcd est le dernier reste non nul;
Pour tout $i$ on a $u_i a + v_i b = r_i,$ donc la dernière de ces relations est la relation de Bezout.

Exemple: Considérons, comme avant 15 et 55

$r_0 = 55, r_1 = 15, u_0 = 1, u_1 = 0, v_0 = 0, v_1 = 1$ ,
$55 = 3\cdot 15 + 10$ , donc $r_2 = 10$ ,
$u_2 = u_0 - 3 u_1 = 1$ ,
$v_2 = v_0 - 3 v_1 = -3$ ,
$15 = 10 + 5$ , donc $r_3 = 5$ ,
$u_3 = u_1 - u_2 = -1$ ,
$v_3 = v_1 - v_2 = 4$ ,
$10 = 2*5$ , donc le pgcd de 15 et 55 est 5,
la relation de Bezout est $-1\cdot 55 + 4\cdot 15 = 5$ .

Exercices

Calculer les relations de Bezout pour les entiers donnés aux exercices 1 et 2.
Calculer l’inverse de $13$ modulo $63$ .

Torus wars

Pour changer, nous allons implanter l’intelligence artificielle d’un jeu: allez voir sa version JavaScript, mais ne passez pas le reste du TD à y jouer!

Le jeu se joue sur une grille $n\times n$ . Votre personnage est bloqué sur une position au hasard à la gauche de la grille, tandis que vos ennemies arrivent de la droite et s’avancent vers vous. Votre personnage est armé, mais un peu myope: il n’a droit que de tirer dans la direction des cases sur la deuxième colonne de la grille; vos adversaires voient un peu plus loin, mais attendent d’être à portée avant de tirer, ce qui vous laisse en théorie le temps de les tuer.

Heureusement, l’arène de jeu est un tore discret (i.e., un doughnut avec pas grand chose à manger): lorsque le projectile sort par le haut, il revient par le bas et inversement. Il est immédiat alors de montrer que si $n$ est premier, vous avez toujours une direction qui vous permet de gagner.

Malheureusement, dans un tore tout projectile qui sort par la droite rentre par la gauche: si vous ratez votre cible le projectile reviendra sur vous et vous tuera.

Faisons un exemple: prenons l’arène $5\times 5$ dans la configuration suivante

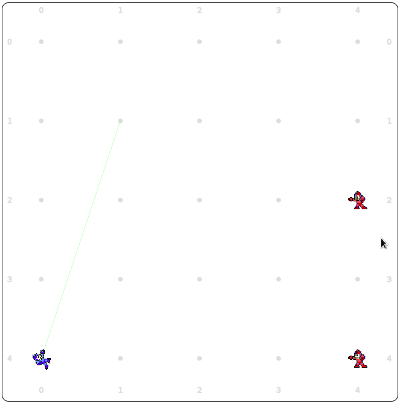
Le joueur est dans la case $(0, 4)$ et tire dans la direction $(1,-3)$ (une direction est juste un vecteur, comme en géométrie, attention cependant: notre axe des ordonnées est renversé, ce qui est souvent le cas en programmation). Le projectile atteint successivement les cases

$(1,1), (2,3), (3,0), (4,2)$

et frappe l’adversaire au milieu de l’écran. En termes mathématiques, nous avons découvert la relation suivante sur des vecteurs de $(\mathbb{Z}/5\mathbb{Z})^2$ :

$\binom{0}{4} + 4\binom{1}{-3} = \binom{4}{2} \mod 5.$

Plus généralement, si le joueur se trouve en position $(0, J_y)$ et l’adversaire en position $(A_x, A_y)$ , nous cherchons une direction $(1,d)$ telle que

$\binom{0}{J_y} + A_x\binom{1}{d} = \binom{A_x}{A_y} \mod n,$

ce qui se traduit en l’équation

$J_y + A_x d = A_y \mod n,$

soit

$d = \frac{A_y - J_y}{A_x} \mod n.$

Pour calculer la direction nous devons donc faire une soustraction, une inversion et une multiplication modulaires. Pour des petits $n$ , cela peut se faire de tête, étant donné qu’en général on peut précalculer $1/A_x$ .

Nous allons écrire en Java une version textuelle simplifiée de ce jeu, où c’est l’ordinateur qui calcule la direction gagnante.

Créez le fichier

import java.util.Vector;

public class Torus {
    /** La vitesse (la periode, en vrai) de defilement 
        du projectile en millisecondes.
    */
    public static int speed = 500;

    /** La dimension du reseau */
    int n;
    /** La position du joueur */
    int player;
    /** La position du mechant */
    int villain_x;
    int villain_y;
    /** La direction de tir */
    int direction;
    /** La position du projectile */
    int bullet_x;
    /** La position du projectile */
    int bullet_y;

    /** Une collection de points du reseau visites, pour rendre
        l'affichage plus clair.  Ca pourrait etre implante plus
        simplement, mais c'est plus robuste comme ca.
    */
    private Vector<String> visited;

    /**
       Constuit une arene de dimension modulus.

       Utilise la methode aim pour determiner la direction de tir.
     */
    public Torus(int modulus) {
        this.n = modulus;
        // Place le joueur et le mechant au hasard
        this.player = (int)(Math.random() * n);
        this.villain_x = 1 + (int)(Math.random() *(n-1));
        this.villain_y = (int)(Math.random() * n);
        // Demande une direction de tire a la methode aim()
        this.direction = this.aim();
        // Place le projectile dans cette direction
        this.bullet_x = 1;
        this.bullet_y = (n + this.player + this.direction) % n;
        this.visited = new Vector<String>();
    }

    /**
       Affiche l'etat courrant de l'arene.  'P' c'est le joueur, 'V'
       le mechant et 'o' le projectile. Les zones traversees par les
       projectiles sont marquees par un '*', les impacts par un '#'.
     */
    public String toString() {
        String s = "      ";
        for (int x = 0 ; x < n ; x++)
            s += String.format("%2d", x) + " ";
        s += "\n\n";
        for (int y = 0 ; y < n ; y++) {
            s += String.format("%2d", y) + "    ";
            for (int x = 0 ; x < n ; x++) {
                boolean bullet = x == bullet_x && y == bullet_y;
                if (x == 0 && player == y)
                    s += bullet ? " # " : " P ";
                else if (x == villain_x && villain_y == y)
                    s += bullet ? " # " : " V ";
                else {
                    if (this.visited.contains(x + "," + y))
                        s += " * ";
                    else
                        s += bullet ? " o " : " . ";
                }
                if (bullet)
                    this.visited.add(x + "," + y);
            }
            s += "\n";
        }
        return s;
    }

    /**
       Fait demarrer le projectile et le deplace toutes les `speed`
       secondes d'un pas dans la direction de tir.

       Utilise la fonction moveBullet pour faire bouger le projectile.
     */
    public void fire() throws InterruptedException {
        int time = 0;
        boolean hit = false;
        while (!hit) {
            Torus.scroll();
            System.out.println(this);
            System.out.println("direction: " + this.direction);
            if (this.bullet_x == 0 && this.bullet_y == this.player ||
                this.bullet_x == this.villain_x && this.bullet_y == this.villain_y) {
                hit = true;
            } else {
                Thread.sleep(Torus.speed);
                this.moveBullet();
            }
        }
        if (this.bullet_x == 0)
            System.out.println("\nYou loose.");
        else
            System.out.println("\nYou win!");
    }

    /**
       Deplace le projectile d'un pas vers la droite dans la direction
       determinee par `this.direction`.
     */
    public void moveBullet() {
        System.out.println("Implantez moveBullet et aim.");
        System.exit(0);
    }

    /**
       Calcule la direction de tir gagnante en fonction the
       `this.player` et de `this.villain`.

       La direction est donnee comme un decalage vertical (positif ou
       negatif) par rapport a la position sur la colonne precedente.

       Utiliser l'algorithme d'Euclide etendu pour resoudre le
       probleme.
     */
    public int aim() {
        return 1;
    }

    /** Nettoye l'ecran */
    public static void scroll() 
    {
        // on fait defiler l'ecran de 24 lignes
        for (int i = 0 ; i < 24 ; i++)
            System.out.println();
    }

    /** Lance le jeu. Il prend un parametre sur la ligne de commande
     * qui indique la dimension de l'arene. Si le parametre est
     * absent, la dimension par defaut est 11.
     */
    public static void main(String[] args) throws InterruptedException {
        int n = 11;
        if (args.length > 0)
            n = Integer.parseInt(args[0]);
        Torus t = new Torus(n);
        t.fire();
    }
}

Ce programme prend une entrée optionnelle sur la ligne de commande, qui est la dimension de l’arène de jeu (11 par défaut). L’affichage de l’arène est fait de façon textuelle comme ci-dessous

       0  1  2  3  4  5  6  7  8  9 10 

 0     .  .  .  .  .  .  .  .  .  .  . 
 1     P  .  .  .  .  .  .  .  .  .  . 
 2     .  o  .  .  .  .  .  .  .  .  . 
 3     .  .  .  .  .  .  .  .  .  .  . 
 4     .  .  .  .  .  .  .  .  .  .  . 
 5     .  .  .  .  .  .  .  .  .  .  . 
 6     .  .  .  .  .  .  .  .  .  .  . 
 7     .  .  .  .  .  .  .  .  .  .  . 
 8     .  .  .  .  .  .  .  .  .  .  V 
 9     .  .  .  .  .  .  .  .  .  .  . 
10     .  .  .  .  .  .  .  .  .  .  . 

direction: 1

Où P représente le joueur, V le méchant et o le projectile. La ligne du bas vous dit en quelle direction pointe votre arme (par défaut, 45 degrés vers le bas). Tant que vous n’implantez pas la méthode moveBullet, le projectile ne bouge pas.

Implantez la méthode moveBullet qui déplace le projectile d’une case horizontalement et de this.direction cases verticalement. Testez le programme et vérifiez que le projectile voyage bien dans la direction.
Implantez la méthode aim qui calcule la direction gagnante.